Niels Henrik Abel (1802- 1829)
Niels Henrik Abel nació el 5 de agosto de 1802 en la isla de Finnöy en la costa sudoccidental de Noruega. Al principio de su instrucción Abel se mostraría como un estudiante indiferente, más bien mediocre y sin indicios de que las matemáticas le despertaran atracción alguna. Era notorio su malestar en la escuela. No obstante, un inesperado cambio se produjo a raíz de la muerte de un condiscípulo ante los malos tratos de un maestro brutal que se excedía con castigos corporales a sus alumnos. El maestro fue entonces relevado en 1818 por un joven matemático de mayor competencia,
Bernt Holmboe (1795-1850), quien incentivó a sus alumnos a resolver por sí mismos problemas de álgebra y de geometría, Abel se familiarizó con resultados científicos superiores conocidos en su época, afanándose en las tres obras de
Leonhard Euler (1707-1803) sobre el cálculo, de
Isaac Newton (1642-1727), de
Carl Friedrich Gauss (1777-1855), y de
Joseph-Louis Lagrange (1736-1813).
En la revista Magazin for Naturvidenskaben que se imprimió en Noruega en 1823, se publicaron algunos breves trabajos de Abel, entre ellos uno en el que aparece por primera vez el planteamiento y la solución de una ecuación integral. En su último año de escuela, Abel se mostraría muy interesado en un importante problema del álgebra, infructuosamente afrontado desde el siglo XVI y que a pesar de los esfuerzos de Lagrange y otros matemáticos, figuraba entre los grandes problemas abiertos, se trataba de hallar la solución mediante radicales de la ecuación algebraica general de quinto grado (o quíntica).
En agosto de 1825 emprendió el viaje al extranjero, aunque antes de partir editó una breve memoria en la que se exhibía la idea de la inversión de las elípticas. En su memoria, sobre el problema de la quíntica, destacó que se debían indagar las condiciones para poder resolver algebraicamente ecuaciones de cualquier grado, preludio de un paréntesis que solventó más tarde Evariste Galois (1811-1832) para sentar las bases de su teoría de ecuaciones mediante la teoría de grupos, mostrando que a cada ecuación corresponde un grupo de sustituciones. Abel investigó la estructura de los grupos conmutativos y mostró que son producto de grupos cíclicos. No obstante, no destacaría en su trabajo el concepto de grupo (ni la noción explícita de subgrupo normal).
August Leopold Crelle era un destacado ingeniero, una de cuyas obras fue el primer ferrocarril prusiano entre Berlín y Postdam y autor también de algunos trabajos matemáticos. Crelle sería un fuerte impulsor de la matemática en Prusia,
fundando en 1825 el
Journal für die reine und angewandte Mathematik (Journal Crelle), revista pionera de matemática pura en el mundo y la más prestigiosa de Alemania. Abel estableció una cordial amistad con Crelle, quien pronto adivinó que Abel era un genio. En los primeros números de la revista editó 7 de sus trabajos; publicando 22 en total en el Journal de Crelle.
El manuscrito de Abel (que contiene el ya conocido como su gran teorema) se refiere a la
extensión del teorema de adición de Euler para integrales elípticas, al caso de integrales de funciones racionales R(x, Y(x)) de la variable x, y de cualquier función algebraica Y(x).
Grosso modo, el teorema enuncia “
cualquier suma de integrales de la forma R(x, y) dx, donde las variables están relacionadas por f(x,y)=0 (f=polinomio en x e y ), puede expresarse en términos de un número fijo p de integrales de ese tipo más términos algebraicos y logarítmicos”. El mínimo número p depende sólo de la ecuación f(x,y)=0, el cual luego sería llamado
género de la misma. Esto muestra que reconoció dicha noción fundamental antes que
G.F. Bernhard Riemann (1826-1866).
Desde hacía tiempo Abel padecía tuberculosis, en la Navidad de 1828 viajó a Fröland. En 1829 empeoró y el 6 de abril falleció. Tenía 26 años. Dos días después de su muerte, una carta de Augusto Crelle, anunciaba que la Universidad de Berlín le había nombrado profesor de matemáticas. Gauss y
Humboldt solicitarían también una cátedra para Abel.
Legendre,
Poisson y
Laplace, escribieron asimismo al
rey de Suecia para que ingresara en la Academia de Estocolmo.
Evariste Galois (1811-1832)
La aportación de Evariste Galois a las matemáticas no es sencilla de entender por la complejidad, incluso para los tiempos actuales, que encierra en su interior. No fue completamente comprendida por los matemáticos de su época, algunos sencillamente la ignoraron, y hasta finales del siglo XIX no se descubrió su profundidad y alcance.
En 1829, siendo todavía estudiante, Galois logró publicar su primer trabajo. Se titulaba 'Demostración de un teorema sobre fracciones continuas periódicas', y apareció en Annales de mathématiques pures et appliquées, de
Joseph Diaz Gergonne.
Galois trabajó durante mucho tiempo en la obtención de una fórmula general válida para ecuaciones de grado 5 y superiores. Normalmente sus esfuerzos concluían en ecuaciones erróneas y más complicadas de resolver que la ecuación original .
Finalmente demostró, casi simultáneamente con
Niels Henrik Abel, la imposibilidad de encontrar una solución general a estas ecuaciones utilizando únicamente la suma, la resta, la multiplicación, la división, la exponenciación y la radicación de los coeficientes (es decir, mediante radicales).
Llegó a la conclusión de que dichas ecuaciones solo pueden resolverse de forma aproximada utilizando técnicas de cálculo numérico. Sin embargo, existen muchas ecuaciones de grado 5 y superiores perfectamente resolubles mediante radicales. Son casos particulares, pero Galois enunció y demostró un teorema (
Teoría de Galois), para identificar dichas ecuaciones. Dice así: «Si en una ecuación polinómica la potencia más alta es un múmero primo y si, supuesto conocidos dos valores de la x, los demás se pueden obtener a partir de ellos usando únicamente la suma, la resta, la multiplicación y la división, entonces la ecuación puede ser resuelta mediante radicales.»
La aportación más importante que Evariste Galois hizo a las matemáticas de su tiempo
fue el concepto de Grupo. El concepto de Grupo fue necesario para encontrar una formulación más general y menos engorrosa que la que porporcionaba el teorema anteriormente citado (identificación de las ecuaciones de grado 5 y superiores resolubles mediante radicales). El concepto no es en absoluto sencillo y Galois llegó a enunciar una condición para que una ecuación polinómica cualquiera pueda ser resoluble madiante radicales. De forma resumida Galois afirmó que "si los coeficientes de una ecuación conforman una estructura de
Grupo de Galois respecto de una determinada operación definida por él y dicho grupo verifica una serie de condiciones también concretadas, entonces la ecuación es resoluble mediante radicales".
Los axiomas de Grupo los definió Galois dentro de su trabajo relativo a resolución de ecuaciones polinómicas. Es decir que, para conseguir un objetivo concreto como fue determinar la resolubilidad mediante radicales de una ecuación polinómica, le fue necesario crear toda una estructura algebraica de enorme aplicación en ramas de la matemática que no tienen nada que ver con el origen de su estudio.
Evariste Galois nació el día 25 de octubre de 1811 en el pueblo de Bourg-la-Reine, situado a escasa distancia de París. A la edad de once años estaba en condiciones de ingresar en el Liceo (escuela superior) Louis-le-Grand de París. Sus resultados escolares de estos años fueron mediocres. Este hecho, unido a su juventud, hizo que los rectores del Liceo le obligaran a repetir el segundo curso. La forma de enseñanza de las matemáticas en el Liceo no difería mucho de la del resto de las asignaturas. Profundizó más en las matemáticas de lo que le exigían y tuvo, por fin, oportunidad de pensar con método, descubrió el desorden imperante dentro del Álgebra y la cantidad de problemas sin resolver que encerraba. Problemas que pasaron a ocupar la mayor parte de su tiempo.
A partir de esta época el joven Galois tenía por fin una meta en su vida: ser matemático. La mejor forma de conseguirlo era ingresar en la
Escuela Politécnica, actualmente el instituto científico más prestigioso de Francia. Para entrar en ella era necesario superar un examen de ingreso. Desgraciadamente, los profesores de la Escuela eran muy semejantes a los del Liceo. Durante el examen oral los examinadores no comprendieron las explicaciones de Evariste, ni el alcance de sus novedosos trabajos en el campo del Álgebra.

Entonces hizo un segundo intento de ingresar en la Escuela Politécnica. Su examinador, el profesor Dinet, supervisor de exámenes durante más de cuarenta años, le hizo una pregunta trivial sobre logaritmos. Sin duda esperaba que Evariste se ciñera a lo conocido hasta entonces sobre el tema, expuesto en el popular libro de texto de Leonhard Euler. Sin embargo, Galois se lanzó a una explicación de sus propias ideas sobre los logaritmos. El viejo Dinet, que fue profesor de Cauchy, no lograba entenderle. Galois lo intentó una y otra vez hasta que definitivamente nervioso e irritado lanzó un borrador a la cabeza del anciano.
De nuevo embebido en sus estudios matemáticos, en febrero de 1830, preparó un trabajo sobre resolución de ecuaciones polinómicas y lo envió a la Academia de Ciencias para optar al Gran Premio de Matemáticas. El trabajo fue aceptado por el gran matemático
Jean-Baptiste Joseph Fourier, pero desgraciadamente murió antes de poder leerlo. El manuscrito se perdió sin dejar rastro.
Evariste se alista en la Guardia Nacional e ingresa en la "Societé des Amis du Peuple". Su estancia en el ejército duró poco ya que ingresó el 4 de diciembre y las baterías de artillería de la Guardia Nacional fueron disueltas el 31 de diciembre del mismo año. La mayor parte de su tiempo en esta época estuvo dedicado a la lucha revolucionaria. Bajo
el régimen de Luis Felipe I tuvieron lugar sus primeros escarceos con la justicia que ya no le abandonarían hasta el fin de sus días, marcado como un agitador político y un peligro para la ley y el orden. Su libertad fue muy breve.
Durante el 14 de julio, Día de la Bastilla, él y un compañero desfilaron por las calles de París armados y vestidos con el uniforme de la artillería de la Guardia Nacional, era ilegal vestir su uniforme y fueron detenidos. Finalmente fue puesto en libertad el 29 de abril de 1832.
El duelo en el que Galois perdió la vida, el adversario era como él, un ardiente republicano. El duelo fue entre amigos y se desarrolló como una especie de ruleta rusa; estando cargada solamente una de las pistolas.
A la mañana siguiente, el viernes 30 de mayo de 1832, en un descampado de las afueras de París, Evariste Galois recibió un disparo en el estómago durante el duelo, que le hizo morir desangrado al día siguiente en un hospital. Fue enterrado en una fosa común.
Los estudios matemáticos de Galois permanecieron incomprendidos hasta mucho tiempo después. Fue en 1846 cuando
Joseph Liouville los publicó completos en una revista matemática francesa. A partir de ese momento comenzaron a influir en los trabajos de los matemáticos posteriores y a ser reconocidos por su importancia. Tanto es así, que hicieron surgir una nueva rama de las Matemáticas llamada Teoría de Grupos y Cuerpos de Galois. Estas ideas fueron consideradas hasta tal punto innovadoras y originales que
el grandísimo matemático alemán Félix Klein dijo de él a finales del siglo XIX: «
En Francia apareció hacia 1800 una nueva estrella de inimaginable brillo en el firmamento de las Matemáticas: Evariste Galois».
Más información:
Nota: mi nick "abelgalois" y el título de este blog son un pequeño homenaje a estos dos grandes matemáticos.
.
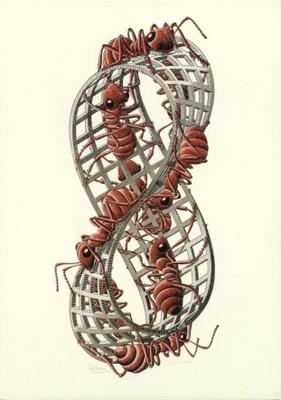 Esta es la cinta que dibujó Escher, una cinta sin fin en la que las hormigas circulan indefinidamente por 'una y otra cara', es decir, por la misma cara. Cinta de Möbius II, 1963, xilografía en tres tintas.
Esta es la cinta que dibujó Escher, una cinta sin fin en la que las hormigas circulan indefinidamente por 'una y otra cara', es decir, por la misma cara. Cinta de Möbius II, 1963, xilografía en tres tintas.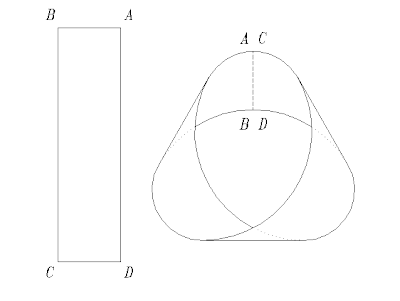 La cinta de Möbius es una superficie tan sencilla como sorprendente. Si cogemos una cinta de vértices ABCD y unimos A con C y B con D, dándole media vuelta, obtenemos una superficie que contra toda apariencia tiene una sola cara, un solo borde y no es orientable.
La cinta de Möbius es una superficie tan sencilla como sorprendente. Si cogemos una cinta de vértices ABCD y unimos A con C y B con D, dándole media vuelta, obtenemos una superficie que contra toda apariencia tiene una sola cara, un solo borde y no es orientable.  Si partimos de un punto de su superficie y comenzamos a colorearla, acabaremos pintado toda la cinta sin haber rebasado el borde. Si seguimos con el dedo uno de los bordes llegamos al punto de partida habiendo recorrido los dos bordes aparentes. Por consiguiente, sólo tiene una cara.
Y lo más sorprendente: si consideramos un vector perpendicular al plano de la cinta en cualquier punto, este cambiará su orientación a medida que recorremos la cinta por su línea central, llegando a convertirse en un vector dirigido en sentido contrario al llegar al mismo punto.
La cinta tiene otras posibilidades de experimentación. Si la cortamos una vez a lo largo de su línea media(linea de puntos del dibujo), obtenemos una sola cinta con cuatro media vueltas, que si que tiene dos caras.
Si partimos de un punto de su superficie y comenzamos a colorearla, acabaremos pintado toda la cinta sin haber rebasado el borde. Si seguimos con el dedo uno de los bordes llegamos al punto de partida habiendo recorrido los dos bordes aparentes. Por consiguiente, sólo tiene una cara.
Y lo más sorprendente: si consideramos un vector perpendicular al plano de la cinta en cualquier punto, este cambiará su orientación a medida que recorremos la cinta por su línea central, llegando a convertirse en un vector dirigido en sentido contrario al llegar al mismo punto.
La cinta tiene otras posibilidades de experimentación. Si la cortamos una vez a lo largo de su línea media(linea de puntos del dibujo), obtenemos una sola cinta con cuatro media vueltas, que si que tiene dos caras.  Si la volvemos a cortar obtenemos dos cintas entrelazadas que tampoco son de Moebius.
Si la volvemos a cortar obtenemos dos cintas entrelazadas que tampoco son de Moebius.  La cinta de Möbius es una superficie tan sencilla como sorprendente. Si cogemos una cinta de vértices ABCD y unimos A con C y B con D, dándole media vuelta, obtenemos una superficie que contra toda apariencia tiene una sola cara, un solo borde y no es orientable.
La cinta de Möbius es una superficie tan sencilla como sorprendente. Si cogemos una cinta de vértices ABCD y unimos A con C y B con D, dándole media vuelta, obtenemos una superficie que contra toda apariencia tiene una sola cara, un solo borde y no es orientable.  Si partimos de un punto de su superficie y comenzamos a colorearla, acabaremos pintado toda la cinta sin haber rebasado el borde. Si seguimos con el dedo uno de los bordes llegamos al punto de partida habiendo recorrido los dos bordes aparentes. Por consiguiente, sólo tiene una cara.
Y lo más sorprendente: si consideramos un vector perpendicular al plano de la cinta en cualquier punto, este cambiará su orientación a medida que recorremos la cinta por su línea central, llegando a convertirse en un vector dirigido en sentido contrario al llegar al mismo punto.
La cinta tiene otras posibilidades de experimentación. Si la cortamos una vez a lo largo de su línea media(linea de puntos del dibujo), obtenemos una sola cinta con cuatro media vueltas, que si que tiene dos caras.
Si partimos de un punto de su superficie y comenzamos a colorearla, acabaremos pintado toda la cinta sin haber rebasado el borde. Si seguimos con el dedo uno de los bordes llegamos al punto de partida habiendo recorrido los dos bordes aparentes. Por consiguiente, sólo tiene una cara.
Y lo más sorprendente: si consideramos un vector perpendicular al plano de la cinta en cualquier punto, este cambiará su orientación a medida que recorremos la cinta por su línea central, llegando a convertirse en un vector dirigido en sentido contrario al llegar al mismo punto.
La cinta tiene otras posibilidades de experimentación. Si la cortamos una vez a lo largo de su línea media(linea de puntos del dibujo), obtenemos una sola cinta con cuatro media vueltas, que si que tiene dos caras.  Si la volvemos a cortar obtenemos dos cintas entrelazadas que tampoco son de Moebius.
Si la volvemos a cortar obtenemos dos cintas entrelazadas que tampoco son de Moebius.  Es increíble el poder de sugerencia que tiene la cinta de Moebius para los artistas. Esta escultura es un ejemplo de cinta de Möbius, en este caso tridimensional, se lo debemos a Max Bill (Winterthur, 1908-Berlín, 1994) pintor, escultor, arquitecto y diseñador gráfico suizo. Uno de los exponentes de los principios vanguardistas de la Bauhaus en Alemania tras el final de la I Guerra Mundial en 1918. Su insistencia en la utilización de una base matemática para toda forma de arte queda reflejada en sus pinturas, que se caracterizan por sus diseños con frecuencia geométricos. Entre 1935 y 1953 creó, en el campo de la escultura, diferentes variaciones sobre el tema del lazo infinito en metal pulido. Por si alguien se pasa por allí, una versión en piedra de esta obra ( Unendliche Schleife) se puede ver en el Centre Pompidou de París.
Es increíble el poder de sugerencia que tiene la cinta de Moebius para los artistas. Esta escultura es un ejemplo de cinta de Möbius, en este caso tridimensional, se lo debemos a Max Bill (Winterthur, 1908-Berlín, 1994) pintor, escultor, arquitecto y diseñador gráfico suizo. Uno de los exponentes de los principios vanguardistas de la Bauhaus en Alemania tras el final de la I Guerra Mundial en 1918. Su insistencia en la utilización de una base matemática para toda forma de arte queda reflejada en sus pinturas, que se caracterizan por sus diseños con frecuencia geométricos. Entre 1935 y 1953 creó, en el campo de la escultura, diferentes variaciones sobre el tema del lazo infinito en metal pulido. Por si alguien se pasa por allí, una versión en piedra de esta obra ( Unendliche Schleife) se puede ver en el Centre Pompidou de París. 





 Un amigo que trabajaba en la empresa de electricidad de Colorado Springs, lo convenció en 1899 para que se trasladase a esa localidad. Allí, comenzó a trabajar en una torre de transmisión de energía de 60 metros de alto denominada “
Un amigo que trabajaba en la empresa de electricidad de Colorado Springs, lo convenció en 1899 para que se trasladase a esa localidad. Allí, comenzó a trabajar en una torre de transmisión de energía de 60 metros de alto denominada “